AC自动机原理

AC（Aho–Corasick）自动机是 以 Trie 的结构为基础，结合 KMP 的思想 建立的自动机，该算法在1975年产生于贝尔实验室，是著名的多模板匹配算法之一。

要搞懂AC自动机，先要有字典树Trie和KMP模式匹配算法的基础知识

字典树 (Trie)

字典树，英文名 trie。顾名思义，就是一个像字典一样的树，是一种哈希树的变种，在统计、排序和保存大量的字符串（但不仅限于字符串）是具有更小的时间复杂度，因此可以应用于搜索引擎系统用于文本词频统计。

它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。

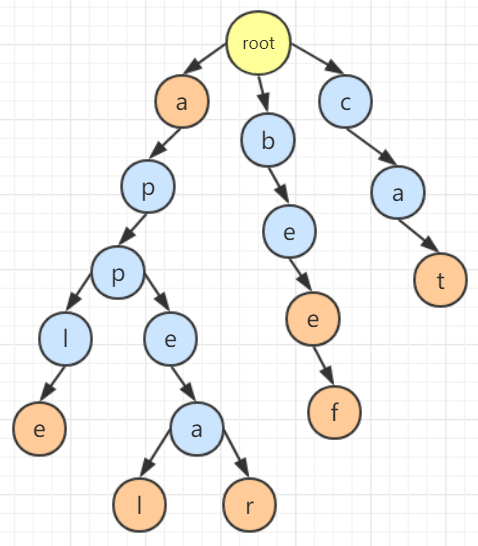
例如我有 “a”、”apple”、”appeal”、”appear”、”bee”、”beef”、”cat” 这 7 个单词，那么就能够组织成如图所示字典树，如果我们要获取 “apple” 这个单词的信息，那么就按顺序访问对应的结点就行啦。

 

字典树的性质

1. 根节点不包含字符，除根节点外每一个节点都只包含一个字符；

2. 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串；

3. 每个节点的所有子节点包含的字符都不相同。

KMP算法

这里假设我们需要从一堆字符串中找出我们需要的字符串在哪里，我们最先想到的最简单的办法可能暴力匹配算法，比如一个子一个子的与子串比对：

一旦匹配失败，我们就跳到下一个字段继续匹配；

失败后，再跳到下一个字符串进行比对。

这个算法很简单，实现起来也很简单，但是最大的问题就是他的时间复杂度，如果运气不好，就像下面这样：

因此效率极低。

而KMP算法避免“调回下一个字符串重新比对”的步骤，也就是说在一次字符串遍历的过程中，就可以比对出子字串。

基本思路就是，当我们发现某个字符串对比不上后，由于知道了前面已经比对过的字符串了，就没有必要将指针递减了，让他永远向前移动。

比如我们比对ABABA；发现只有后面的C是对不上的，是不是可以将子串中的AB移动到主串的第二个AB继续对比呢？

那么问题在于，我们怎么知道跳过多少字符呢，这里就要用到KMP中定义的next数组了。

我们这里先不管next数组，我们先看KMP的功能。

当子串与主串匹配失败后，会查看匹配失败前一个字符的对应的next值，我们看到B为2，那么就可移动子串直接跳过前面的两个字符。

这里的2代表“可以跳过”的字符个数，也就是AB字符我们不需要匹配了，很显然，这里是没啥问题的，因为我们看到主串上的AB确实跟子串的AB一致。

然后继续匹配后面的字符就好了。

由于不再需要回退主串中的指针，只需要一次遍历就可以完全匹配，效率自然比之前的暴力匹配快的多，下面我们通过动画看看KMP的具体匹配逻辑。

NEXT数组的定义

上面我们看到，next的数值代表的是在匹配失败的时候，子串中可以跳过的字符个数。

如果是2，我们就可以跳过前两个字符的比较，但是凭什么这么做呢？我们看到，因为前面匹配的两个AB和我们跳过的两个AB实际上是一样的。

换句话说，子串的两个前缀完全是一样的，因为前缀和后缀AB长度为2。所以，next的本质也就是寻找子串中相同前后缀的字符长度。并且规定了，一定是最长的前后缀。

下面的子串中，虽然A有好几个，但是不是最长的，因为有更长ABA所以第二个ABA的长度就为3。

我们以ABABC为例，来说一下next数组的计算。

首先第一个A字符，应该没有比他还短的前后缀了，所以A的next直接为0。

接着是AB两个字符，应该没有比他俩还短的前后缀了，所以AB的next也为0。

接着是ABA前三个字符，由于A是共同的前后缀，所以next为1。

接着是ABAB前四个字符，由于AB是共同的前后缀，所以next为2。

接着是ABABC前五个字符，找不到共同的前后缀，所以next为0。

这样我们就计算得到了ABABC的整个next数组了。

所以，计算next数组前后缀的长度，可以用递推的方式不断的利用已经掌握的信息，计算出前后缀的next值 ，来避免重复的计算。

假设我们已经知道相同的AB的前后缀是2了，如果下一个字符依然相同，那么就是+1；

那如果下一个字符无法与前面的构成更长的相同的前后缀，我们便可以找到上一个相同的ABA的前后缀，所以找到左边ABA的前后缀为1。

然后我们继续寻找更长的前后缀，所以AB可以构成更长的前后缀，也就是1+1为2；

寻找的过程动画

AC自动机在实现上要依托于Trie树并借鉴了KMP模式匹配算法的核心思想。实际上你可以把KMP算法看成每个节点都仅有一个孩子节点的AC自动机。

AC自动机及其运行原理

初识AC自动机

AC自动机的基础是Trie树。和Trie树不同的是，树中的每个结点除了有指向孩子的指针（或者说引用），还有一个fail指针，它表示输入的字符与当前结点的所有孩子结点都不匹配时(注意，不是和该结点本身不匹配)，自动机的状态应该转移到的结点。fail指针的功能可以类比于KMP算法中next数组的功能。

我们现在来看一个用目标字符串集合{“abd”,”abdk”, “abchijn”, “chnit”, “ijabdf”, “ijaij”}构造出来的AC自动机

上图是一个构建好的AC自动机，其中根结点不存储任何字符，根结点的fail指针为null。虚线表示该结点的fail指针的指向，所有表示字符串的最后一个字符的结点外部都用红圈表示，我们称该结点为这个字符串的终结结点。每个结点实际上都有fail指针，但为了表示方便，我们将指向根结点的 fail虚线都未画出。

从上图中的AC自动机，我们可以看出一个重要的性质：每个结点的fail指针表示由根结点到该结点所组成的字符序列的所有后缀和整个目标字符串集合（也就是整个Trie树）中的所有前缀 两者中最长公共的部分。

比如图中，由根结点到目标字符串“ijabdf”中的 ‘d’组成的字符序列“ijabd”的所有后缀在整个目标字符串集{abd,abdk, abchijn, chnit, ijabdf, ijaij}的所有前缀中最长公共的部分就是abd，而图中d结点（字符串“ijabdf”中的这个d）的fail正是指向了字符序列abd的最后一个字符。

AC自动机的运行过程：

1）表示当前结点的指针指向AC自动机的根结点，即curr = root

2）从文本串中读取（下）一个字符

3）从当前结点的所有孩子结点中寻找与该字符匹配的结点，若成功：判断当前结点以及当前结点fail指向的结点是否表示一个字符串的结束，若是，则将文本串中索引起点记录在对应字符串保存结果集合中（ 索引起点 = 当前索引 – 字符串长度 +1）。curr指向该孩子结点，继续执行第2步；若失败：执行第4步。

4）若fail == null（说明目标字符串中没有任何字符串是输入字符串的前缀，相当于重启状态机）curr = root, 执行步骤2，

否则，将当前结点的指针指向fail结点，执行步骤3)

现在，我们来一个具体的例子加深理解，初始时当前结点为root结点，我们现在假设文本串text = “abchnijabdfk”。

图中的实曲线表示了整个搜索过程中的当前结点指针的转移过程，结点旁的文字表示了当前结点下读取的文本串字符。比如初始时，当前指针指向根结点时，输入字符‘a’,则当前指针指向结点a，此时再输入字符‘b’,自动机状态转移到结点b,……，以此类推。图中AC自动机的最后状态只是恰好回到根结点。

需要说明的是，当指针位于结点b（图中曲线经过了两次b,这里指第二次的b，即目标字符串“ijabdf”中的b）,这时读取文本串字符下标为9的字符（即‘d’）时，由于b的所有孩子结点（这里恰好只有一个孩子结点）中存在能够匹配输入字符d的结点,那么当前结点指针就指向了结点d，而此时该结点d的fail指针指向的结点又恰好表示了字符串“abc”的终结结点（用红圈表示），所以我们找到了目标字符串“abc”一次。这个过程我们在图中用虚线表示，但状态没有转移到“abd”中的d结点。

在输入完所有文本串字符后，我们在文本串中找到了目标字符串集合中的abd一次，位于文本串中下标为7的位置；目标字符串ijabdf一次，位于文本串中下标为5的位置。

构造AC自动机的方法与原理

构造的基本方法

首先我们将所有的目标字符串插入到Trie树中，然后通过广度优先遍历为每个结点的所有孩子节点的fail指针找到正确的指向。

确定fail指针指向的问题和KMP算法中构造next数组的方式如出一辙。具体方法如下

1）将根结点的所有孩子结点的fail指向根结点，然后将根结点的所有孩子结点依次入列。

2）若队列不为空：

2.1）出列，我们将出列的结点记为curr, failTo表示curr的fail指向的结点，即failTo = curr.fail

2.2) a.判断curr.child[i] == failTo.child[i]是否成立，

成立：curr.child[i].fail = failTo.child[i]，

不成立：判断 failTo == null是否成立

成立： curr.child[i].fail == root

不成立：执行failTo = failTo.fail，继续执行2.2）

b.curr.child[i]入列，再次执行再次执行步骤2)

若队列为空:结束

通过一个例子来理解构造AC自动机的原理

每个结点fail指向的解决顺序是按照广度优先遍历的顺序完成的，或者说层序遍历的顺序进行的，也就是说我们是在解决当前结点的孩子结点fail的指向时，当前结点的fail指针一定已指向了正确的位置。

以上图所示为例，我们要解决结点x1的某个孩子结点y的fail的指向问题。已知x1.fail指向x2，依据x1结点的fail指针的含义，我们可知红色实线椭圆框内的字符序列必然相等，且表示了最长公共部分。依据y.fail的含义，如果x2的某个孩子结点和结点y表示的字符相等，那么y.fail就该指向它。

如果x2的孩子结点中不存在结点y表示的字符，这个时候该怎么办？由于x2.fail指向x3，根据x2.fail的含义，我们可知绿色方框内的字符序列必然相等。显然，如果x3的某个孩子结点和结点y表示的字符相等，那么y.fail就该指向它。

如果x3的孩子结点中不存在结点y表示的字符，我们可以依次重复这个步骤，直到xi结点的fail指向null，这时说明我们已经到了最顶层的根结点，这时，我们只需要让ｙ.fail = root即可。

构造的过程的核心本质就是，已知当前结点的最长公共前缀的前提下，去确定孩子结点的最长公共前缀。这完全可以类比于KMP算法的next数组的求解过程。

确定图中h结点fail指向的过程

现在我们假设我们要确定图中结点c的孩子结点h的fail指向。图中每个结点都应该有表示fail的虚线，但为了表示方便，所有指向根结点的 fail虚线均未画出。

左图中，蓝色实线框住的结点的fail都已确定。现在我们应该怎样找到h.fail的正确指向？由于且结点c的fail已知（c结点为h结点的父结点），且指向了Trie树中所有前缀与字符序列‘a’‘b’‘c’的所有后缀（“bc”和“c”）的最长公共部分。现在我们要解决的问题是目标字符串集合的所有前缀中与字符序列‘a’‘b’‘c’ ‘h’的所有后缀的最长公共部分。显然c.fail指向的结点的孩子结点中存在结点h，那么h.fail就应该指向c.fail的孩子结点h，所以右图表示了h.fail确定后的情况。

确定图中i.fail指向的过程

确定i.fail的指向时，显然h.fail(h指图中i的父结点的那个h)已指向了正确的位置。也就是说我们现在知道了目标字符串集合所有前缀中与字符序列‘a’‘b’‘c’ ‘h’的所有后缀在Trie树中的最长前缀是‘c’‘h’。显然从图中可知h.fail的孩子结点是没有i结点（这里h.fail只有一个孩子结点n）。字符序列‘c’‘h’的所有后缀在Trie树中的最长前缀可由h.fail的fail得到，而h.fail的fail指向root（依据本博客中画图的原则，这条fail虚线并未画出）,root的孩子结点中存在表示字符i的结点,所以结果如右图所示。

AC自动机的java代码实现

package datastruct;
 
import java.util.ArrayList;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.List;
import java.util.Map.Entry;
 
public class AhoCorasickAutomation {
    /*本示例中的AC自动机只处理英文类型的字符串，所以数组的长度是128*/
    private static final int ASCII = 128;
     
    /*AC自动机的根结点，根结点不存储任何字符信息*/
    private Node root;
     
    /*待查找的目标字符串集合*/
    private List<String> target;
     
    /*表示在文本字符串中查找的结果，key表示目标字符串， value表示目标字符串在文本串出现的位置*/
    private HashMap<String, List<Integer>> result;
     
    /*内部静态类，用于表示AC自动机的每个结点，在每个结点中我们并没有存储该结点对应的字符*/
    private static class Node{
         
        /*如果该结点是一个终点，即，从根结点到此结点表示了一个目标字符串，则str != null, 且str就表示该字符串*/
        String str;
         
        /*ASCII == 128, 所以这里相当于128叉树*/
        Node[] table = new Node[ASCII];
         
        /*当前结点的孩子结点不能匹配文本串中的某个字符时，下一个应该查找的结点*/
        Node fail;
         
        public boolean isWord(){
            return str != null;
        }
         
    }
     
    /*target表示待查找的目标字符串集合*/
    public AhoCorasickAutomation(List<String> target){
        root = new Node();
        this.target = target;
        buildTrieTree();
        build_AC_FromTrie();
    }
     
    /*由目标字符串构建Trie树*/
    private void buildTrieTree(){
        for(String targetStr : target){
            Node curr = root;
            for(int i = 0; i < targetStr.length(); i++){
                char ch = targetStr.charAt(i);
                if(curr.table[ch] == null){
                    curr.table[ch] = new Node();
                }
                curr = curr.table[ch];
            }
            /*将每个目标字符串的最后一个字符对应的结点变成终点*/
            curr.str = targetStr;
        }
    }
     
    /*由Trie树构建AC自动机，本质是一个自动机，相当于构建KMP算法的next数组*/
    private void build_AC_FromTrie(){
        /*广度优先遍历所使用的队列*/
        LinkedList<Node> queue = new LinkedList<Node>();
         
        /*单独处理根结点的所有孩子结点*/
        for(Node x : root.table){
            if(x != null){
                /*根结点的所有孩子结点的fail都指向根结点*/
                x.fail = root;
                queue.addLast(x);/*所有根结点的孩子结点入列*/
            }
        }
         
        while(!queue.isEmpty()){
            /*确定出列结点的所有孩子结点的fail的指向*/
            Node p = queue.removeFirst();
            for(int i = 0; i < p.table.length; i++){
                if(p.table[i] != null){
                    /*孩子结点入列*/
                    queue.addLast(p.table[i]);
                    /*从p.fail开始找起*/
                    Node failTo = p.fail;
                    while(true){
                        /*说明找到了根结点还没有找到*/
                        if(failTo == null){
                            p.table[i].fail = root;
                            break;
                        }
                         
                        /*说明有公共前缀*/
                        if(failTo.table[i] != null){
                            p.table[i].fail = failTo.table[i];
                            break;
                        }else{/*继续向上寻找*/
                            failTo = failTo.fail;
                        }
                    }
                }
            }
        }
    }
     
    /*在文本串中查找所有的目标字符串*/
    public HashMap<String, List<Integer>> find(String text){
        /*创建一个表示存储结果的对象*/
        result = new HashMap<String, List<Integer>>();
        for(String s : target){
            result.put(s, new LinkedList<Integer>());
        }
         
        Node curr = root;
        int i = 0;
        while(i < text.length()){
            /*文本串中的字符*/
            char ch = text.charAt(i);
             
            /*文本串中的字符和AC自动机中的字符进行比较*/
            if(curr.table[ch] != null){
                /*若相等，自动机进入下一状态*/
                curr = curr.table[ch];
                 
                if(curr.isWord()){
                    result.get(curr.str).add(i - curr.str.length()+1);
                }
                 
                /*这里很容易被忽视，因为一个目标串的中间某部分字符串可能正好包含另一个目标字符串，
                 * 即使当前结点不表示一个目标字符串的终点，但到当前结点为止可能恰好包含了一个字符串*/
                if(curr.fail != null && curr.fail.isWord()){
                    result.get(curr.fail.str).add(i - curr.fail.str.length()+1);
                }
                 
                /*索引自增，指向下一个文本串中的字符*/
                i++;
            }else{
                /*若不等，找到下一个应该比较的状态*/
                curr = curr.fail;
                 
                /*到根结点还未找到，说明文本串中以ch作为结束的字符片段不是任何目标字符串的前缀，
                 * 状态机重置，比较下一个字符*/
                if(curr == null){
                    curr = root;
                    i++;
                }
            }
        }
        return result;
    }
     
     
    public static void main(String[] args){
        List<String> target = new ArrayList<String>();
        target.add("abcdef");
        target.add("abhab");
        target.add("bcd");
        target.add("cde");
        target.add("cdfkcdf");
         
        String text = "bcabcdebcedfabcdefababkabhabk";
         
        AhoCorasickAutomation aca = new AhoCorasickAutomation(target);
        HashMap<String, List<Integer>> result = aca.find(text);
         
        System.out.println(text);
        for(Entry<String, List<Integer>> entry : result.entrySet()){
            System.out.println(entry.getKey()+" : " + entry.getValue());
        }
         
    }
}